torquemoment of inertia

0906 Moment of Inertia

I=∫r2dm\begin{aligned} I = \int r^2 dm \end{aligned}

Examples

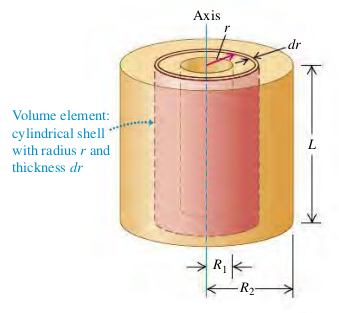
(9.10) Figure 9.23 shows a hollow cylinder of uniform mass density r with length L, inner radius R1R_1, and outer radius R2R_2. (It might be a steel cylinder in a printing press.) Using integration, find its moment of inertia about its axis of symmetry.
Graph

Solution

I=∫r2dm=∫R1R2r2ρ(2πrLdr)=2πρL∫R1R2r3dr=24πρL(R24−R14)=12πρL(R22−R12)(R22+R12)(1)\begin{aligned} I &= \int r^2 dm = \int_{R_1}^{R_2} r^2 \rho (2\pi r L dr)\\ &= 2\pi \rho L \int_{R_1}^{R_2} r^3 dr\\ &= \frac{2}{4} \pi \rho L(R_2^4 - R_1^4)\\ &= \frac{1}{2} \pi \rho L(R_2^2 - R_1^2)(R_2^2 + R_1^2) &\text{(1)}\\ \end{aligned}

The cylinder's volume is V=πL(R22−R12)V = \pi L (R_2^2 - R_1^2), so its total mass is

M=ρV=πL(R22−R12)(2)\begin{aligned} M &= \rho V = \pi L (R_2^2 - R_1^2) &\text{(2)} \end{aligned}

Substituting Eq. (2) to Eq. (1), we see that

I=12M(R22+R12)\begin{aligned} I &= \frac{1}{2} M(R_2^2 + R_1^2) \end{aligned}

If the cylinder is solid, with outer radius R2=RR_2 = R and inner Radius R1=0R_1 = 0, its moment of inertia is

I=12MR2\begin{aligned} I &= \frac{1}{2}MR^2 \end{aligned}

If the cylinder wall is very thin, we have R1≈R2=RR_1 \approx R_2 = R and the moment of inertia is

I=MR2\begin{aligned} I &= MR^2 \end{aligned}

Exercises

(Quiz) Use Integration and dI=r2dmd I = r^2 dm to find the moment of inertia for a meter stick about 10cm point.

Solution

I=∫r2dm=∫−xL−x(r2ML)dr=112ML2+M(L2−x)2\begin{aligned} I &= \int r^2 dm\\ &= \int_{-x}^{L-x} (r^2 \frac{M}{L})dr\\ &= \frac{1}{12}ML^2 + M(\frac{L}{2} - x)^2 \end{aligned}

L=1mL = 1m, and x=0.1mx = 0.1m, so we see

I=112M+M(12−0.1)2=0.243M\begin{aligned} I &= \frac{1}{12} M + M(\frac{1}{2} - 0.1)^2\\ &= 0.243M \end{aligned}