A skier is skiing along a frictionless circular track with radius of R=10m. Find the height where she leaves the surface of hemisphere.
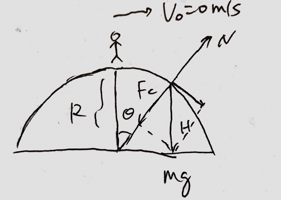
Solution
First, let's find final velocity vf before she leaves the surface, at the moment she leave the surface, the normal force is zero. N=0
∑FcRmvf2vf=Wcosθ−N=mgcosθ−0=gRcosθ
Second, accoriding to conservation of energy,
21mv02+mgR0+mgR⇒H=21mvf2+mgH=21m(gRcosθ)2+mg⋅Rcosθcosθ=32=Rcosθ=10⋅32≈6.3m