2202 Calculating Electric Flux

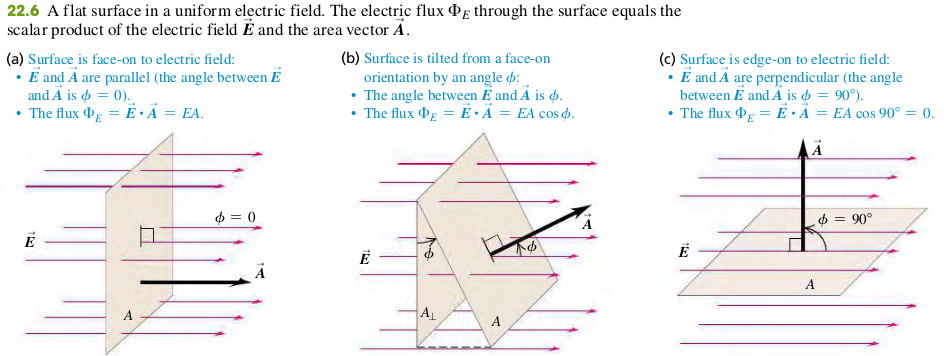
Flux of a Uniform Electric Field

The electric flux through a flat area AA perpendicular to a uniform electric field E⃗\vec{E} is the product of the field magnitude EE and the area AA:

ΦE=EA\begin{aligned} \Phi_E = EA \end{aligned}

In terms of vector area A⃗\vec{A} perpendicular to the area, we can write the electric flux as the scalar product of E⃗\vec{E} and A⃗\vec{A}

ΦE=E⃗⋅A⃗(22.3)\begin{aligned} \Phi_E = \vec{E} \cdot \vec{A} \quad \bold{(22.3)} \end{aligned}

Graph

Flux of a Nonuniform Electric Field

ΦE=∫Ecos⁡ϕdA=∫E⊥dA=∫E⃗⋅dA⃗(22.5)\begin{aligned} \Phi_E = \int E\cos \phi dA = \int E_\perp dA = \int \vec{E}\cdot d\vec{A} \quad \bold{(22.5)} \end{aligned}

ϕ\phi - Angle between E⃗\vec{E} and normal to surface
dAdA - Element of surface area
E⊥E_\perp - Component of E⃗\vec{E} perpendicular to surface

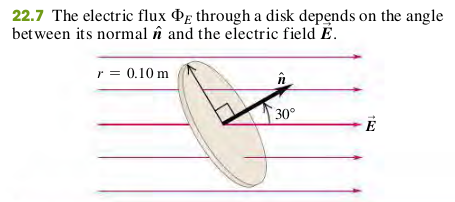
EXAMPLE 22.1 ELETRIC FLUX THROUGH A DISK

A disk of radius 0.10 m is oriented with its normal unit vector n^\hat n at 30°\degree to a uniform electric field E⃗\vec{E} of magnitude 2.0×103N/C2.0\times 10^3 N/C (Fig. 22.7). (Since this isn’t a closed surface, it has no “inside”
or “outside.” That’s why we have to specify the direction of n^\hat n in the figure.)
(a) What is the electric flux through the disk?
(b) What is the flux through the disk if it is turned so that n^\hat n is perpendicula to E⃗\vec{E}?
(c) What is the flux through the disk if n^\hat n is parallel to E⃗\vec{E}?
The electric flux through a disk depends on the angle between its normal and the electric field.

Solution

a. The area A=π(0.10m)2=0.0314m2A = \pi(0.10m)^2 = 0.0314 m^2, and the angle between E⃗\vec{E} and A⃗=An^\vec{A} = A\hat n is ϕ=30°\phi = 30\degree, so from Eq. (22.1),

ΦE=EAcos⁡ϕ=(2.0×103N/C)(0.0314m2)(cos⁡30°)=54N⋅m2/C\begin{aligned} \Phi_E &= EA\cos\phi = (2.0 \times 10^3 N/C) (0.0314 m^2)(\cos 30\degree)\\ &= 54 N\cdot m^2/C \end{aligned}

b. THe normal to the disk is now perpendiculaa to E⃗\vec{E}, so ϕ=90°\phi = 90 \degree, and ΦE=0\Phi_E = 0.
c. THe normal to the disk is parallel to E⃗\vec{E}, so ϕ=0\phi = 0 and cos⁡ϕ=1\cos \phi = 1:

ΦE=EAcos⁡ϕ=(2.0×103N/C)(0.0314m2)(1)=63N⋅m2/C\begin{aligned} \Phi_E &= EA\cos\phi = (2.0 \times 10^3 N/C) (0.0314 m^2)(1)\\ &= 63 N\cdot m^2/C \end{aligned}

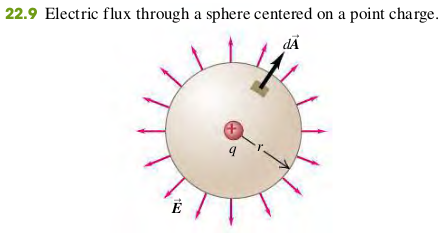
EXAMPLE 22.2 ELETRIC FLUX THROUGH A SPHERE

A point charge q=+3.0μCq = +3.0 \mu C is surrounded by an imaginary sphere of radius r=0.20r = 0.20 m centered on the charge (Fig. 22.9). Find the resulting electric flux through the sphere.
The electric flux through a sphere centered on a point charge

Solution

The surface is not flat and the electric field is not uniform, so to calculate the electric flux we must use the general definition, Eq. (22.5). Because the sphere is centered on the point charge, at any point on the spherical surface, E⃗\vec{E} is directed out of the sphere perpendicular to the surface. The positive direction for both n^\hat n and E⊥E_\perp is outward, so E⊥=EE_\perp = E, and the flux through a surface element dAdA is E⃗⋅A⃗=EdA\vec{E} \cdot \d\vec{A} = E dA.

ΦE=EA=q4πϵ0r2⋅4πr2=qϵ0=3.0×10−68.85×1012=3.4×105N⋅m2/C\begin{aligned} \Phi_E &= EA = \frac{q}{4\pi\epsilon_0 r^2} \cdot 4\pi r^2 = \frac{q}{\epsilon_0}\\ &= \frac{3.0 \times 10^{-6}}{8.85 \times 10^{12}} = 3.4 \times 10^5 N\cdot m^2/C \end{aligned}