2402 Capacitors in Series And Parallel

Capacitors in Series

The reciprocal of the equivalent capcitance of a series combination equals the sume of the reciprocal of the individual capacitors.

1Ceq=1C1+1C2+1C3+⋯(24.5)\begin{aligned} \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \cdots \quad \bold{(24.5)} \end{aligned}

Caution
The magnitude of charge is the same on all plates of all capacitors in series combination. However, the potential difference of the individual capacitors are not the same unless their individual capacitances are the same.

Capacitors in Parallel

The equivalent capcitance of a parallel combination equals the sum of the individual capacitances.

Ceq=C1+C2+C3+⋯(24.7)\begin{aligned} C_{eq} &= C_1 + C_2 + C_3 + \cdots \quad\bold{(24.7)} \end{aligned}

Caution
The potential difference are the same for all capacitors in a parallel combination, however, the chareges on individual capacitors are not the same unless their individual capacitances are the same.

Exercises

14

24.14 Figure E24.14 shows a system of four capacitors, where the potential difference across ab is 50.0 V. (a) Find the equivalent capacitance of this system between a and b. (b) How much charge is stored by this combination of capacitors? (c) How much charge is stored in each of the 10.0μF10.0 \mu F and the 9μF9 \mu F capacitors?
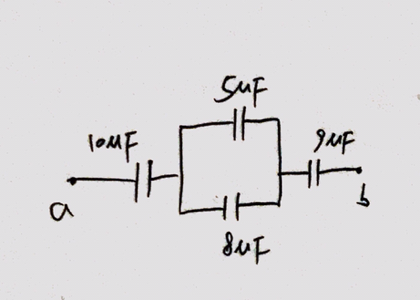
Graph

Solution

a. The equivalent capacitance is

Ceq=1110μF+15μF+8μF+19μF=3.47μF\begin{aligned} C_{eq} &= \frac{1}{\frac{1}{10\mu F} + \frac{1}{5\mu F + 8\mu F} + \frac{1}{9\mu F}}\\ &= 3.47 \mu F \end{aligned}

b. The stored charge is

Q=CeqVab=3.47μF×50.0V=1.74×10−4C\begin{aligned} Q &= C_{eq} V_{ab} = 3.47 \mu F \times 50.0 V\\ &= 1.74 \times 10^{-4}C \end{aligned}

c. The charge stored in the 10.0μF10.0 \mu F and the 9μF9 \mu F capacitors are both Q=1.74×10−4CQ = 1.74 \times 10^{-4}C.