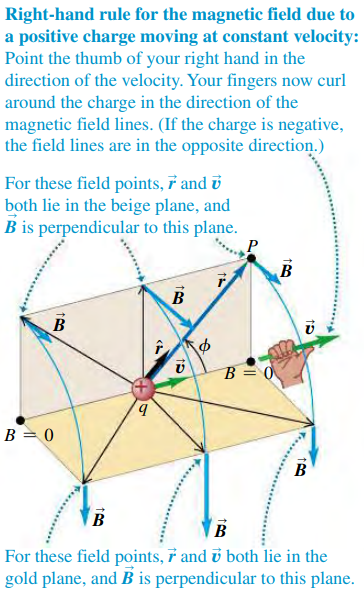
2801 Magnetic Field of a Moving Charge

Moving Charge: Vector Magnetic Field

The magnitude of B⃗\vec{B} is proportional to ∣q∣|q| and to 1/r21/r^2. But the direction of B⃗\vec{B} is not along the line from source point to the field point. Instead, B⃗\vec{B} is perpendicular to the plane containing this line and the particle's velocity vector v⃗\vec{v}. Furthermore, the field magnitude BB is also proportionalto the particles's speed vv and to the sine of the angle ϕ\phi.

B⃗=μ04πqv⃗×r^r2B=μ04π∣q∣vsin⁡ϕr2\begin{aligned} \vec{B} &= \frac{\mu_0}{4\pi} \frac{q\vec{v} \times\hat r}{r^2}\\ B &= \frac{\mu_0}{4\pi} \frac{|q|v \sin{\phi}}{r^2} \end{aligned}

r^\hat r - unit vector that points from the source point to the field point.
rr - distance from point charge to where field is measured.
qq - Charge
v⃗\vec{v} - Velocity
μ0\mu_0 - magnetic constant.

Graph

EXAMPLE 28.1 Forces Between Two Moving Protons

Two protons move parallel to the x-axis in opposite directions (Fig. 28.2) at the same speed vv (small compared to the speed of light cc). At the instant shown, find the electric and magnetic forces on the upper proton and compare their magnitudes.
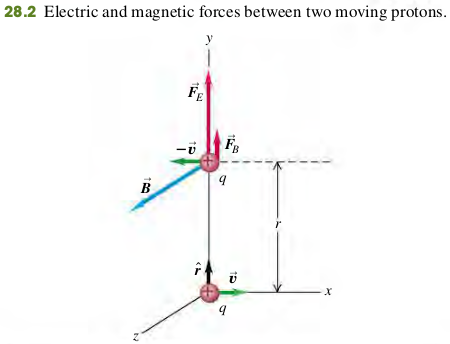
Graph

Solution

Coulomb's Law gives the electric force FEF_E on the upper proton. The magnetic force law gives the magnetic force on the upper proton.
The forces are replusive, so FEF_E is vertically upward (+y-direction).

FE⃗=14πϵ0q2r2j^\begin{aligned} \vec{F_E} &= \frac{1}{4\pi \epsilon_0} \frac{q^2}{r^2} \jhat \end{aligned}

The velocity of the lower proton is v⃗=vi^\vec{v} = v \ihat. From right hand rule for the cross product v⃗×r^\vec{v} \times \hat r, the B⃗\vec{B} field due to the lowe proton at the position of the upper proton is in the +z-direction. The magnetic field is

B⃗=μ04πq(vi^)×j^r2=μ04πqvr2k^\begin{aligned} \vec{B} = \frac{\mu_0}{4\pi} \frac{q(v\ihat) \times \jhat}{r^2} = \frac{\mu_0}{4\pi} \frac{qv }{r^2} \khat \end{aligned}

The velocity of the upper proton is −v⃗=−vi^-\vec{v} = -v \ihat. so the magnetic force on it is

FB⃗=q(−v⃗)×B⃗=q(−vi^)×μ04πqvr2k^=μ04πq2v2r2j^\begin{aligned} \vec{F_B} &= q(-\vec{v}) \times \vec{B} \\ &= q(-v\ihat) \times \frac{\mu_0}{4\pi} \frac{qv }{r^2} \khat\\ &= \frac{\mu_0}{4\pi} \frac{q^2 v^2}{r^2} \jhat \end{aligned}

The magnetic interaction in this situation is also repulsive. The ratio of the force magnitude is

FBFE=μ0q2v2/4πr2q2/4πϵ0r2=μ0ϵ0v2=v2c2\begin{aligned} \frac{F_B}{F_E} &= \frac{\mu_0 q^2 v^2/4\pi r^2}{q^2 /4\pi \epsilon_0 r^2}\\ &= \mu_0\epsilon_0 v^2 \\ &= \frac{v^2}{c^2} \end{aligned}

When vv is small in comparison to the speed of the light, the magnetic force is much smaller than the electric force.